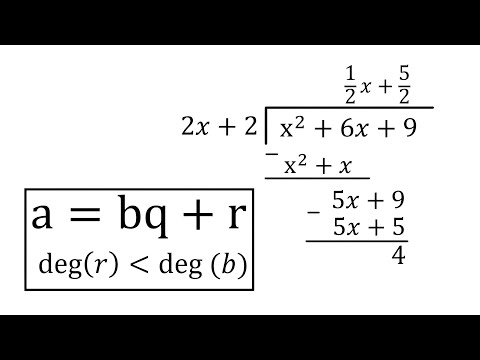
เนื้อหา
- ส่วนพหุนามยาว: วัตถุประสงค์
- ส่วนพหุนามยาว: กระบวนการ
- ส่วนพหุนามพหุนาม: วัตถุประสงค์
- กองสังเคราะห์พหุนาม: กระบวนการ
การหารพหุนามยาวเป็นวิธีที่ใช้ในการลดความซับซ้อนของฟังก์ชันพหุนามด้วยการหารพหุนามด้วยอีกระดับเดียวกันหรือต่ำกว่าพหุนาม มันจะมีประโยชน์เมื่อลดความซับซ้อนของการแสดงออกพหุนามด้วยมือเพราะมันแบ่งปัญหาที่ซับซ้อนเป็นปัญหาที่มีขนาดเล็กลง บางครั้งพหุนามถูกหารด้วยปัจจัยเชิงเส้นในรูปแบบทั่วไปขวาน + b ในกรณีนี้วิธีลัดที่เรียกว่าการแบ่งสังเคราะห์สามารถนำมาใช้เพื่อลดความซับซ้อนของการแสดงออกเหตุผล โดยทั่วไปวิธีนี้ใช้เพื่อค้นหารากหรือศูนย์ของพหุนาม
ส่วนพหุนามยาว: วัตถุประสงค์
การหารแบบยาวด้วยพหุนามเกิดขึ้นเมื่อคุณต้องการทำให้ปัญหาการหารที่เกี่ยวข้องกับการแยกแบบสองส่วนง่ายขึ้น วัตถุประสงค์ของการหารแบบยาวที่มีหลายชื่อมีความคล้ายคลึงกับการหารแบบยาวที่มีจำนวนเต็ม เพื่อค้นหาว่าตัวหารเป็นปัจจัยของการจ่ายเงินปันผลหรือไม่และถ้าไม่ตัวหารหลังตัวหารจะถูกรวมเข้ากับเงินปันผล ความแตกต่างหลักตรงนี้คือตอนนี้คุณหารด้วยตัวแปร
ส่วนพหุนามยาว: กระบวนการ
ตัวหารในส่วนยาวพหุนามคือส่วนและเงินปันผลคือตัวเศษของพหุนาม ปัญหาการหารถูกตั้งค่าเหมือนกับปัญหาการหารจำนวนเต็มโดยตัวหารที่อยู่ด้านนอกของวงเล็บทางซ้ายและเงินปันผลภายในวงเล็บ หารเทอมนำของเงินปันผลโดยเทอมนำของตัวหารและวางผลลัพธ์ไว้ด้านบนของวงเล็บ ผลลัพธ์นั้นจะถูกคูณด้วยตัวหารจากนั้นลบผลลัพธ์จากเงินปันผลโดยดำเนินการกับเงื่อนไขใด ๆ ที่ไม่ได้มีส่วนร่วมในการลบ กระบวนการนี้จะดำเนินต่อไปจนกว่าคุณจะได้รับศูนย์เป็นคำตอบหรือไม่สามารถแยกปัจจัยนำของตัวหารเข้าสู่เงินปันผลได้อีกต่อไป
ส่วนพหุนามพหุนาม: วัตถุประสงค์
การแยกโพลิโนเมียลเป็นรูปแบบที่ง่ายขึ้นของการแบ่งพหุนามที่ใช้เฉพาะในกรณีของการหารโดยปัจจัยเชิงเส้นซึ่งเป็น monomial มันถูกใช้มากที่สุดเพื่อค้นหารากของพหุนาม มันไม่ได้อยู่ในวงเล็บหารและตัวแปรที่ใช้ในการหารพหุนามยาวและมุ่งเน้นไปที่สัมประสิทธิ์ของพหุนามในคำถาม วิธีนี้จะทำให้ขั้นตอนการหารสั้นลงและอาจทำให้เกิดความสับสนน้อยกว่าการหารพหุนามทั่วไป
กองสังเคราะห์พหุนาม: กระบวนการ
แทนที่จะเป็นตัวยึดการหารแบบทั่วไปเช่นเดียวกับการแบ่งแบบยาวในการแบ่งแบบสังเคราะห์คุณต้องใช้เส้นตั้งฉากที่หันหน้าไปทางขวาทำให้มีที่ว่างสำหรับการแบ่งหลายแถว เฉพาะค่าสัมประสิทธิ์ของพหุนามที่ถูกหารอยู่ภายในวงเล็บที่ด้านบน การทดสอบตัวเลขที่สงสัยว่าเป็นศูนย์เกี่ยวข้องกับการวางตัวเลขนั้นไว้นอกวงเล็บถัดจากค่าสัมประสิทธิ์พหุนาม สัมประสิทธิ์แรกดำเนินการลงด้านล่างสัญลักษณ์การหารไม่เปลี่ยนแปลง จากนั้นศูนย์ทดสอบจะถูกคูณด้วยค่าที่ยกลงและผลลัพธ์จะถูกเพิ่มเข้าไปในค่าสัมประสิทธิ์ถัดไป ค่าที่ยกลงก่อนหน้านี้จะถูกคูณด้วยผลลัพธ์ใหม่จากนั้นเพิ่มค่าสัมประสิทธิ์ถัดไป ดำเนินการต่อกระบวนการนี้ไปจนถึงสัมประสิทธิ์สุดท้ายเผยให้เห็นผลลัพธ์ของศูนย์หรือส่วนที่เหลือ หากมีส่วนที่เหลืออยู่ศูนย์ทดสอบจะไม่เป็นศูนย์จริงของพหุนาม