ความแตกต่างระหว่างค่าสัมบูรณ์และสมการเชิงเส้น

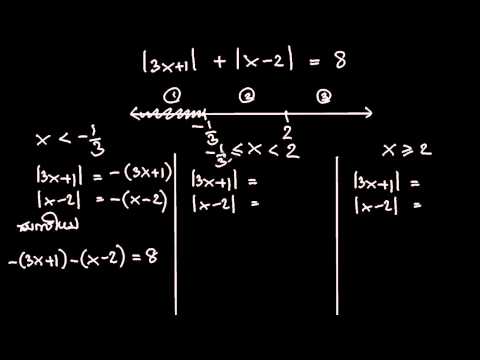
เนื้อหา

• โดเมนและพิสัย
• กราฟ
• จำนวนตัวแปร
• โซลูชั่น

ค่าสัมบูรณ์เป็นฟังก์ชันทางคณิตศาสตร์ที่ใช้ค่าบวกของตัวเลขใด ๆ ที่อยู่ภายในเครื่องหมายค่าสัมบูรณ์ซึ่งถูกวาดเป็นแถบแนวตั้งสองแถบ ตัวอย่างเช่นค่าสัมบูรณ์ของ -2 - เขียนเป็น | -2 | - เท่ากับ 2 ในทางตรงกันข้ามสมการเชิงเส้นอธิบายความสัมพันธ์ระหว่างสองตัวแปร ตัวอย่างเช่น y = 2x +1 บอกคุณว่าการคำนวณ y สำหรับค่าใด ๆ ของ x คุณเพิ่มค่าเป็นสองเท่าของ x แล้วเพิ่ม 1

โดเมนและพิสัย

โดเมนและพิสัยเป็นศัพท์ทางคณิตศาสตร์ที่อธิบายค่าอินพุต (x) ที่เป็นไปได้ทั้งหมดและค่าเอาต์พุต (y) ที่เป็นไปได้ทั้งหมดตามลำดับของฟังก์ชัน ตัวเลขใด ๆ สามารถป้อนเข้าในค่าสัมบูรณ์หรือสมการเชิงเส้นและดังนั้นโดเมนของทั้งสองรวมถึงจำนวนจริงทั้งหมด เนื่องจากค่าสัมบูรณ์ไม่สามารถลบได้ค่าที่เล็กที่สุดที่เป็นไปได้คือศูนย์ ในทางตรงกันข้ามสมการเชิงเส้นสามารถอธิบายค่าที่เป็นลบศูนย์หรือบวก เป็นผลให้ช่วงของฟังก์ชันค่าสัมบูรณ์เป็นศูนย์และจำนวนบวกทั้งหมดในขณะที่ช่วงของสมการเชิงเส้นคือตัวเลขทั้งหมด

กราฟ

กราฟของฟังก์ชันค่าสัมบูรณ์มีลักษณะเป็น "v" ส่วนปลายของ "v" ตั้งอยู่ที่ค่า y ต่ำสุดของฟังก์ชั่น (เว้นแต่จะมีเครื่องหมายลบที่ด้านหน้าของแถบค่าสัมบูรณ์ซึ่งในกรณีนี้กราฟจะมีการกลับหัว "v" โดยมีปลายที่ ฟังก์ชั่นค่า y สูงสุด) ในทางตรงกันข้ามกราฟของสมการเชิงเส้นเป็นเส้นตรงที่อธิบายโดยสมการ y = mx + b โดยที่ m คือความชันของเส้นและ b คือจุดตัดแกน y (เช่นที่เส้นตัดผ่านแกน y)

จำนวนตัวแปร

สมการค่าสัมบูรณ์สามารถมีตัวแปรสองตัวได้เช่นเดียวกับสมการเชิงเส้นที่ทำ แต่พวกเขายังสามารถมีเพียงหนึ่งตัวแปร ตัวอย่างเช่น y = | 2x | + 1 คือกราฟของสมการค่าสัมบูรณ์คล้ายกับสมการเชิงเส้น y = 2x +1 ในรูปแบบ (แม้ว่ากราฟจะดูแตกต่างกันมากดังที่อธิบายไว้ข้างต้น) ตัวอย่างของสมการค่าสัมบูรณ์ที่มีเพียงหนึ่งตัวแปรคือ | x | = 5

โซลูชั่น

สมการเชิงเส้นและสมการค่าสัมบูรณ์สองตัวแปรประกอบด้วยสองตัวแปรดังนั้นจึงไม่สามารถแก้ไขได้หากไม่มีสมการที่สอง สำหรับสมการค่าสัมบูรณ์กับตัวแปรหนึ่งตัวโดยปกติจะมีสองวิธี ในสมการค่าสัมบูรณ์ | x | = 5, คำตอบคือ 5 และ -5, เนื่องจากค่าสัมบูรณ์ของแต่ละหมายเลขนั้นคือ 5 ตัวอย่างที่ซับซ้อนมากขึ้นมีดังนี้: | 2x + 1 | -3 = 4. ในการแก้สมการเช่นนี้ก่อนอื่นให้จัดเรียงใหม่เพื่อให้ค่าสัมบูรณ์เป็นของตัวเองที่ด้านหนึ่งของเครื่องหมายเท่ากับ ในกรณีนี้หมายถึงการบวก 3 เข้ากับทั้งสองข้างของสมการ อัตราผลตอบแทนนี้ | 2x + 1 | = 7. ขั้นตอนต่อไปคือการลบแถบค่าสัมบูรณ์และตั้งค่ารุ่นหนึ่งเท่ากับหมายเลขเดิม 7 และรุ่นอื่นเท่ากับค่าลบของ i.e. -7 สุดท้ายแก้แต่ละนิพจน์แยกกัน ในตัวอย่างนี้เรามี 2x + 1 = 7 และ 2x + 1 = -7 ซึ่งทำให้ x = 3 หรือ -4 ง่ายขึ้น