วิธีหาสมการของเส้นสัมผัส

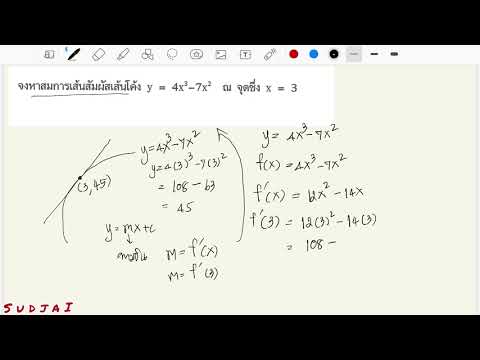
เส้นสัมผัสสัมผัสกับเส้นโค้งที่จุดหนึ่งและจุดเดียวเท่านั้น สมการของเส้นสัมผัสสามารถหาได้โดยใช้วิธีการตัดความชันหรือวิธีจุดความชันสมการความชัน - จุดตัดในรูปแบบพีชคณิตคือ y = mx + b โดยที่ "m" คือความชันของเส้นตรงและ "b" คือจุดตัดแกน y ซึ่งเป็นจุดที่เส้นสัมผัสตัดผ่านแกน y สมการความชันจุดในรูปแบบพีชคณิตคือ y - a0 = m (x - a1) โดยที่ความชันของเส้นคือ "m" และ (a0, a1) เป็นจุดบนเส้น

สร้างความแตกต่างของฟังก์ชั่นที่กำหนด f (x) คุณสามารถค้นหาอนุพันธ์โดยใช้หนึ่งในหลายวิธีเช่นกฎพลังงานและกฎผลิตภัณฑ์ กฎการใช้พลังงานระบุว่าสำหรับฟังก์ชันพลังงานของรูปแบบ f (x) = x ^ n, ฟังก์ชันอนุพันธ์, f (x), เท่ากับ nx ^ (n-1) โดยที่ n คือค่าคงที่จำนวนจริง ตัวอย่างเช่นอนุพันธ์ของฟังก์ชัน f (x) = 2x ^ 2 + 4x + 10 คือ f (x) = 4x + 4 = 4 (x + 1)

กฎผลิตภัณฑ์ระบุอนุพันธ์ของผลิตภัณฑ์ของทั้งสองฟังก์ชันคือ f1 (x) และ f2 (x) เท่ากับผลิตภัณฑ์ของฟังก์ชันแรกคูณด้วยอนุพันธ์ของสองและผลิตภัณฑ์ของฟังก์ชันที่สองคูณอนุพันธ์ของ เป็นครั้งแรก ตัวอย่างเช่นอนุพันธ์ของ f (x) = x ^ 2 (x ^ 2 + 2x) คือ f '(x) = x ^ 2 (2x + 2) + 2x (x ^ 2 + 2x) ซึ่งทำให้ 4x ง่ายขึ้น ^ 3 + 6x ^ 2

ค้นหาความชันของเส้นสัมผัส หมายเหตุอนุพันธ์อันดับหนึ่งของสมการ ณ จุดที่ระบุคือความชันของเส้น ในฟังก์ชั่น f (x) = 2x2 ^ 2 + 4x + 10 ถ้าคุณถูกขอให้หาสมการของเส้นสัมผัสที่ x = 5 คุณจะเริ่มด้วยความชัน, m ซึ่งเท่ากับค่าของ อนุพันธ์ที่ x = 5: f (5) = 4 (5 + 1) = 24

รับสมการของเส้นสัมผัสที่จุดใดจุดหนึ่งโดยใช้วิธีจุดความชัน คุณสามารถแทนที่ค่าที่กำหนดของ "x" ในสมการเดิมเพื่อรับ "y"; นี่คือจุด (a0, a1) สำหรับสมการความชันจุด, y - a0 = m (x - a1) ในตัวอย่าง f (5) = 2 (5) ^ 2 + 4 (5) + 10 = 50 + 20 + 10 = 80 ดังนั้นจุด (a0, a1) คือ (5, 80) ในตัวอย่างนี้ ดังนั้นสมการกลายเป็น y - 5 = 24 (x - 80) คุณสามารถจัดเรียงใหม่และแสดงในรูปแบบความชัน - จุดตัด: y = 5 + 24 (x - 80) = 5 + 24x - 1920 = 24x - 1915