วิธีการสร้างกราฟบันทึก

กราฟบันทึกหรือที่เรียกว่ากราฟกึ่งลอการิทึมอย่างเป็นทางการคือกราฟที่ใช้สเกลเชิงเส้นในหนึ่งแกนและสเกลลอการิทึมบนแกนอื่น ๆ มันมีประโยชน์ในด้านวิทยาศาสตร์สำหรับการพล็อตจุดข้อมูลของตัวแปรสองตัวซึ่งหนึ่งในตัวแปรนั้นมีช่วงของค่าที่ใหญ่กว่าตัวแปรอื่น ๆ โดยการพล็อตข้อมูลด้วยวิธีนี้เราสามารถสังเกตความสัมพันธ์ในข้อมูลที่ไม่ชัดเจนหากตัวแปรทั้งสองถูกพล็อตเชิงเส้น

กำหนดลอการิทึม สำหรับสมการ x = b ^ y เราจะบอกว่า y คือลอการิทึมของ x ถึงฐาน b ดังนั้นถ้า x = b ^ y ดังนั้น y = logb (x)

สร้างสเกลเชิงเส้นและลอการิทึม เครื่องหมายในระดับเชิงเส้นจะแสดงแต่ละหน่วยและมีป้ายกำกับ 1, 2, 3, 4 และอื่น ๆ เครื่องหมายบนมาตราส่วนลอการิทึมแสดงพลังของฐานลอการิทึม ตัวอย่างเช่นสเกลลอการิทึมที่มีฐาน 10 จะมีป้ายกำกับ 10, 100, 1,000 และอื่น ๆ

ฟังก์ชั่นแผนที่บนกราฟเชิงเส้น ทั้งเครื่องชั่ง x และ y วัดหน่วยเดียวกัน ในภาพประกอบ y = f (x) ในสีเขียวจึงเป็นเส้นตรงที่มีความชัน 1 Y = log10 (x) ในสีน้ำเงินตัดกับแกน x ที่ x = 1 และมีความชันเป็นบวกที่เข้าใกล้ 0 y = 10 ^ x สีแดงตัดแกน y ที่ y = 1 และมีความชันเป็นบวกที่เข้าหาอนันต์



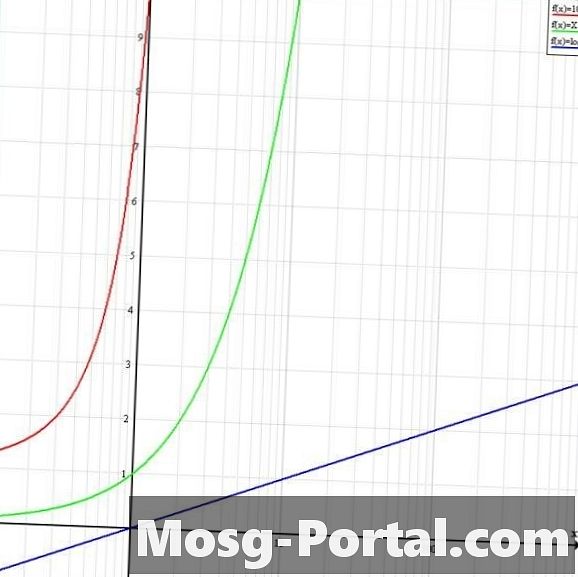
ใช้กราฟบันทึกการทำงาน กราฟบันทึกประเภทนี้มีแกน y ที่มีสเกลเชิงเส้นและแกน x ที่มีสเกลลอการิทึม สเกลของแกน x จึงถูกบีบอัดโดยปัจจัย 10 ^ x ที่สัมพันธ์กับแกน y ในภาพประกอบ y = log10 (x) เป็นสีน้ำเงินตอนนี้คล้ายกับเส้น y = x บนกราฟเชิงเส้น Y = 10 ^ x สีแดงตัดแกน y ที่ x = 10 และมีความชันเป็นบวกที่เข้าหาอนันต์ Y = x เป็นสีเขียวตอนนี้ดูเหมือนว่า y = 10 ^ x บนกราฟเชิงเส้น



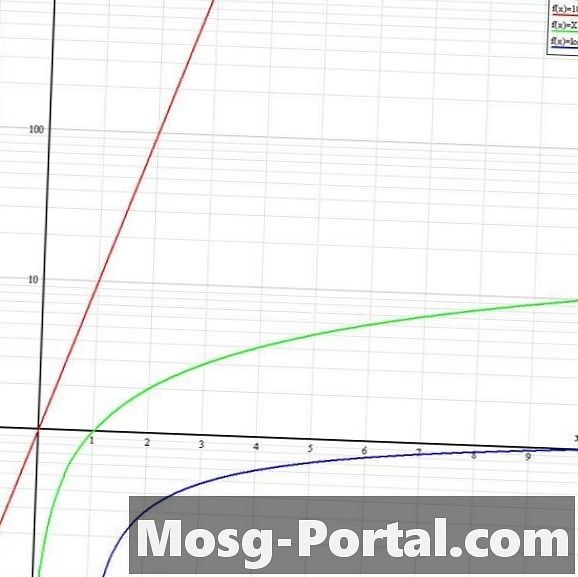
ใช้กราฟบันทึกการทำงาน กราฟบันทึกประเภทนี้มีแกน y ที่มีสเกลลอการิทึมและแกน x ที่มีสเกลเชิงเส้น สเกลของแกน x จึงถูกขยายด้วยปัจจัย 10 ^ x ที่สัมพันธ์กับแกน y ในภาพประกอบ y = 10 ^ x ในสีแดงดูเหมือน y = x บนกราฟเส้นตรง Y = x ในสีเขียวดูเหมือน y = log10 (x) บนกราฟเชิงเส้นและ y = log10 (x) อยู่ด้านล่างของแกน x ด้วยความชันบวกและเข้าใกล้แกน x asymptotically