
เนื้อหา
เพื่อให้รูปร่างสองรูปสมภาคกันแต่ละคนจะต้องมีจำนวนด้านเท่ากันและมุมของพวกเขาต้องเท่ากัน วิธีที่ง่ายที่สุดในการพิจารณาว่ารูปร่างสองแบบสมกันคือหมุนรูปร่างใดรูปร่างหนึ่งหรือไม่จนกว่ามันจะถูกเรียงเป็นแถวกับอีกรูปร่างหนึ่งหรือเพียงวางรูปร่างซ้อนทับกันเพื่อดูว่าปลายด้านใดยื่นออกมาหรือไม่ ถ้าคุณไม่สามารถย้ายรูปร่างได้คุณสามารถใช้สูตรเพื่อตรวจสอบว่ารูปร่างนั้นสอดคล้องกันหรือไม่
แวดวงที่สอดคล้องกัน
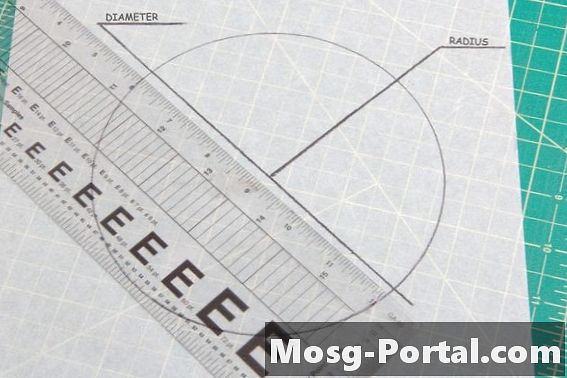
••• Ray Robert Green / Demand Mediaวงกลมทั้งหมดมีมุมเท่ากัน 360 องศา ปัจจัยเดียวในการพิจารณาความสอดคล้องของวงกลมสองวงคือการเปรียบเทียบขนาดของพวกเขา เส้นผ่านศูนย์กลางเป็นเส้นตรงผ่านจุดศูนย์กลางของวงกลมจากขอบถึงขอบในขณะที่รัศมีของวงกลมคือความยาวจากกึ่งกลางไปจนถึงขอบด้านนอก การวัดสิ่งเหล่านี้บนวงกลมทั้งสองจะพิสูจน์ได้ว่าสอดคล้องกันหรือไม่
สี่เหลี่ยมด้านขนาน
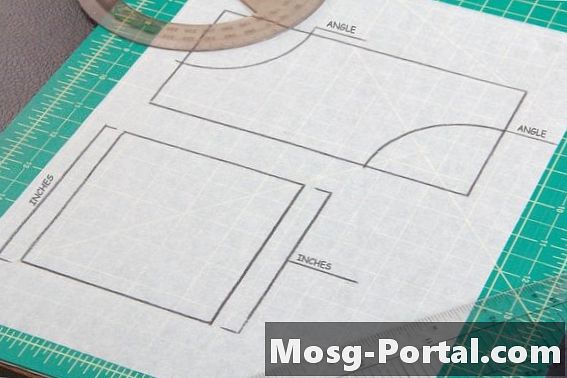
สี่เหลี่ยมด้านขนานมีด้านคู่ขนานสองคู่เช่นสี่เหลี่ยมและสี่เหลี่ยม ด้านตรงข้ามหรือมุมของรูปสี่เหลี่ยมด้านขนานมีขนาดเท่ากันดังนั้นจึงจำเป็นต้องทำการวัดมุมหรือด้านข้างสองรูปแบบบนรูปสี่เหลี่ยมด้านขนานหนึ่งอันจากด้านข้างของแต่ละคู่เพื่อเปรียบเทียบความสอดคล้องกับรูปร่างอื่น
สามเหลี่ยม
••• Ray Robert Green / Demand Mediaเพื่อหาความสอดคล้องของรูปสามเหลี่ยมคุณต้องกำหนดขนาดของทุกมุมหรือด้านข้างเนื่องจากทั้งสามอาจแตกต่างกัน มีสามหลักที่สามารถใช้เพื่อระบุรูปสามเหลี่ยมสมภาคกันได้ SSS postulate คือเมื่อคุณวัดทั้งสามด้านไปยังแต่ละสามเหลี่ยม ASA สมมุติว่าถ้ามุมใดมุมหนึ่งและด้านเชื่อมต่อตรงกับสามเหลี่ยมอื่น ๆ พวกมันจะสมภาคกัน SAS postulate ทำตรงข้ามวัดสองด้านและมุมเชื่อมต่อเพื่อเปรียบเทียบกับสามเหลี่ยมอื่น ๆ
ทฤษฎีบทสำหรับสามเหลี่ยมที่สอดคล้องกัน

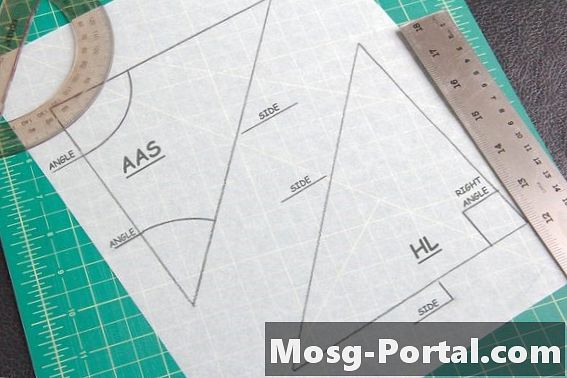
ทฤษฎีบททั้งสองมีประโยชน์สำหรับการค้นหาสามเหลี่ยมที่สอดคล้องกัน ทฤษฎีบท AAS บอกว่าหากมุมทั้งสองและด้านที่ไม่ได้เชื่อมต่อทั้งสองนั้นเท่ากับสามเหลี่ยมอีกมุมหนึ่งพวกมันจะสมภาคกัน ทฤษฎีบท Hypotenuse-Leg ใช้กับสามเหลี่ยมที่มีมุม 90 องศาหรือ "ขวา" เพียงมุมเดียวเท่านั้น นี่คือเมื่อคุณวัดด้านตรงข้ามมุมฉาก - ด้านตรงข้ามมุม 90 องศา - และอีกด้านหนึ่งของสามเหลี่ยมเพื่อเปรียบเทียบกับรูปร่างอื่น